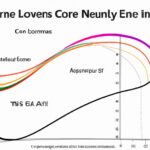
The Gini coefficient is a measure of income inequality within a population. It ranges from 0 to 1, with 0 indicating perfect equality and 1 representing extreme inequality. The coefficient is calculated by plotting the cumulative share of population against the cumulative share of income. A higher coefficient value implies greater inequality, meaning that a small percentage of the population holds a majority of the wealth. The Gini coefficient is often used by economists and policymakers to assess the level of income disparity in a country and to design policies that promote more equitable distribution of wealth.
Table of Contents
- Alternatives to Gini coefficient
- Calculation of Gini coefficient
- Interpretation of Gini coefficient
- Limitations of Gini coefficient
- Use of Gini coefficient
(Gini Coefficient | Lorenz curve | Values of Gini Coefficient | Learn Economics on Ecoholics)
The Gini coefficient is a statistical measure used to gauge income inequality within a defined population. It is named after an Italian statistician named Corrado Gini, who developed the concept in 1912. The coefficient is represented by a value between 0 and 1, with 0 indicating perfect equality and 1 indicating extreme inequality.
To calculate the Gini coefficient, income data is organized in ascending order. Then, a Lorenz curve is constructed by plotting the cumulative percentage of income on the y-axis against the corresponding cumulative percentage of the population on the x-axis. The Gini coefficient is derived by measuring the area between the Lorenz curve and a hypothetical line of perfect equality.
A Gini coefficient of 0 denotes a situation where every individual in the population possesses the exact same income. This scenario represents perfect income equality. On the other hand, a coefficient of 1 signifies that one individual or group possesses all the income while others have none. This extreme inequality is representative of a Gini coefficient of 1.
The Gini coefficient is widely used by economists, policymakers, and sociologists to study income disparities and assess the effectiveness of government policies aimed at reducing inequality. For example, a decrease in the Gini coefficient over time would indicate a reduction in income inequality, while an increase would suggest a rise in inequality.
While the Gini coefficient provides valuable insights into income inequality, it does have limitations. It does not account for non-income factors such as wealth disparities or access to education and healthcare. Additionally, it is sensitive to population size and can be influenced by outliers or extreme values.
In conclusion, the Gini coefficient is a statistical tool used to measure income inequality within a population. With its range from 0 to 1, it provides a clear indication of the level of inequality present. While it has its limitations, it remains an important measure for policymakers and researchers striving to understand and address income disparities.
Alternatives to Gini coefficient
The Gini coefficient is a widely used measure of income inequality. It is a single number that summarizes the degree of income inequality within a society. However, it is not the only measure available, and there are several alternatives that can provide a different perspective on income inequality.
One alternative to the Gini coefficient is the Theil index. This index measures the average income loss that individuals face due to inequality. It takes into account both the level of inequality and the distribution of income across individuals. The Theil index has the advantage of being sensitive to changes in inequality at different points in the income distribution.
Another alternative is the Atkinson index. This index incorporates a parameter that reflects society’s aversion to inequality. It allows policymakers to trade off between inequality and average income. The Atkinson index is particularly useful in analyzing policy changes that have distributional consequences.
The Palma ratio is another alternative to the Gini coefficient. It compares the income share of the richest 10% of the population with the income share of the poorest 40%. The Palma ratio provides a simple and intuitive measure of inequality, focusing on the extremes of the income distribution.
The Hoover index is a measure of relative inequality that compares the proportion of total income going to the middle 60% of the population with the proportions going to the top and bottom 20%. The Hoover index captures the extent to which income is concentrated in the tails of the distribution.
Lastly, the coefficient of variation is an alternative measure that examines the variation in income across individuals. It is calculated as the ratio of the standard deviation of incomes to the mean income. The coefficient of variation provides a measure of relative inequality that is independent of changes in the mean income.
These alternative measures to the Gini coefficient offer different ways of understanding income inequality. While the Gini coefficient is a valuable tool, it is essential to consider these alternatives to gain a more comprehensive picture of inequality within a society. Each measure has its strengths and weaknesses, and policymakers must carefully consider which measure is most appropriate for their analysis and policy goals. By incorporating these alternative measures, the understanding of income inequality can be enriched, leading to more informed and effective policy interventions.
Calculation of Gini coefficient
Calculation of Gini coefficient was developed by Italian statistician Corrado Gini in the early 20th century. It is a widely used measure of inequality in a distribution. The Gini coefficient ranges from 0 to 1, where 0 represents perfect equality and 1 represents maximal inequality.
To calculate the Gini coefficient, first, the data must be ordered from lowest to highest. Next, the cumulative percentage of individuals and the cumulative percentage of income or wealth for each corresponding individual must be determined.
To calculate the Gini coefficient, subtract the area under the Lorenz curve (which represents the actual distribution of income or wealth) from the area under the line of perfect equality (which represents a perfectly equal distribution). The resulting value is then divided by the area under the line of perfect equality. This can be expressed in the following formula:
Gini coefficient = (A – B) / A
Here, A represents the area under the line of perfect equality and B represents the area under the Lorenz curve.
The value obtained from this calculation can be interpreted as the proportion of inequality that exists in the distribution. A Gini coefficient of 0 indicates perfect equality, while a coefficient of 1 signifies maximal inequality.
In practical terms, the Gini coefficient can be calculated using statistical software or by hand using a step-by-step approach. The latter involves calculating the areas of each section between the Lorenz curve and the line of perfect equality by breaking it down into smaller trapezoids.
The Gini coefficient is widely used by economists, policymakers, and researchers to measure and compare income and wealth inequality within and across countries. It provides a comprehensive summary of the distribution of income or wealth and serves as an important tool for analyzing differences in economic well-being.
By understanding how to calculate the Gini coefficient, individuals can gain valuable insights into inequality and use this information to inform policy decisions aimed at reducing disparities and promoting social justice. The Gini coefficient is an indispensable tool in understanding and addressing income and wealth inequality in societies around the world.
Interpretation of Gini coefficient
Definition of Gini coefficient
The Gini coefficient, a statistical measure commonly used in economics, is used to represent income inequality within a population. It provides a numerical value between 0 and 1, with 0 indicating perfect equality and 1 indicating maximum inequality. The interpretation of the Gini coefficient allows policymakers and researchers to understand the distribution of income or wealth and the disparities that may exist within a society.
A Gini coefficient close to 0 signifies a more egalitarian society, where everyone has a similar income or wealth. On the other hand, a coefficient closer to 1 indicates significant disparities, with a few individuals holding a large portion of the total income or wealth.
Interpreting Gini coefficients requires a thorough understanding of the economic context in which they are derived. It is crucial to consider the factors that contribute to income inequality, such as educational opportunities, social mobility, and government policies. For example, a country with high levels of educational attainment and accessible healthcare may have a lower Gini coefficient compared to a country with limited educational opportunities.
Gini coefficients can also be used to compare income distribution across different regions or time periods. By examining changes in the Gini coefficient over time, policymakers can evaluate the effectiveness of policies aimed at reducing income inequality. Additionally, comparing Gini coefficients between countries allows for a global perspective on income disparities and can inform international development efforts.
While the Gini coefficient provides a useful summary measure of income inequality, it is important to supplement its interpretation with other indicators and qualitative analysis. Factors such as unemployment rates, social welfare programs, and household debt levels can provide additional insights into the economic well-being of a population.
In conclusion, the Gini coefficient is a valuable tool for assessing income inequality within a population. Understanding its interpretation requires considering social, economic, and cultural factors that influence income disparities. By examining Gini coefficients, policymakers and researchers can gain insights into income distribution trends and make informed decisions to address inequality. However, it is essential to complement this measure with a broader understanding of the socioeconomic context to gain a complete understanding of income disparities.
Limitations of Gini coefficient
The Gini coefficient, a widely used measure of income inequality, has its limitations. One limitation is that it only considers income distribution and ignores other factors like wealth, education, and access to healthcare. This narrow focus may not provide a comprehensive picture of inequality in a society.
Another limitation is that the Gini coefficient does not take into account differences in cost of living. Two individuals with the same income can have vastly different standards of living depending on where they live. Therefore, using the Gini coefficient alone may not accurately reflect the level of inequality experienced by individuals in different regions or countries.
The Gini coefficient also assumes a linear relationship between income distribution and welfare. It does not account for non-economic factors that can influence well-being, such as social support systems or cultural norms. Therefore, it may not accurately capture the overall impact of inequality on individuals’ quality of life.
Additionally, the Gini coefficient does not distinguish between different income sources, such as wages, investments, or social benefits. This can result in a skewed representation of inequality, as different sources of income may have different distribution patterns. A more nuanced analysis that considers these different sources would provide a more accurate assessment of inequality.
Furthermore, the Gini coefficient is based on the assumption that income distribution follows a specific probability distribution function, such as the Lorenz curve. However, income distribution in reality is often more complex and may not fit these theoretical assumptions. This can limit the accuracy and reliability of the Gini coefficient as a measure of inequality.
Lastly, the Gini coefficient is a snapshot in time and does not capture changes in inequality over time. It cannot account for factors like social mobility or shifts in income distribution patterns. Therefore, using the Gini coefficient alone may not provide a complete understanding of the dynamics and trends of inequality in a society.
In conclusion, while the Gini coefficient is a useful measure for assessing income inequality, it has its limitations. Its narrow focus, failure to consider non-economic factors, and assumptions about income distribution can limit its accuracy and applicability. To gain a more comprehensive understanding of inequality, it is important to consider additional measures and factors.
Use of Gini coefficient
The Gini coefficient is a statistical tool used to measure income inequality within a population. It provides a numerical representation of the distribution of wealth or income among the individuals in the society. The coefficient takes a value between 0 and 1, where 0 represents perfect equality and 1 represents extreme inequality.
One of the significant uses of the Gini coefficient is in comparing income disparities between different countries. By calculating the coefficient for various nations, policymakers can gain insights into the level of inequality within each country and make informed decisions on measures to address the issue. For example, a high Gini coefficient indicates a higher level of income inequality, which may suggest the need for policies that aim to redistribute wealth and promote inclusivity.
Furthermore, the Gini coefficient is also valuable for analyzing income distribution within a specific population, such as a city or state. By measuring inequality over time, policymakers and researchers can track changes in income disparities and assess the effectiveness of policies implemented to reduce inequality. This data can support evidence-based decision-making and help identify areas of improvement.
Moreover, the Gini coefficient is frequently used by economists and researchers to study the relationship between income inequality and various socio-economic factors. For example, studies have shown that higher levels of income inequality can have negative impacts on social cohesion, economic growth, and even health outcomes. By examining the Gini coefficient in conjunction with other variables, researchers can gain a deeper understanding of the complex nature of inequality and its consequences.
In addition to its academic and research applications, the Gini coefficient is also a useful tool for businesses and organizations. By understanding the income distribution within their target market, companies can tailor their products and services to better meet the needs of different income groups. This knowledge can lead to more effective marketing strategies and increased customer satisfaction.
In conclusion, the Gini coefficient is an essential tool for measuring income inequality. Its applications range from informing policy decisions to guiding business strategies. By providing a quantitative measure of income distribution, the coefficient contributes to a better understanding of societal disparities and facilitates efforts towards a more equitable world.