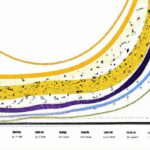
Interpreting the Lorenz curve is crucial to understanding income inequality. The curve plots the cumulative share of income against the population percentile. A perfectly equal distribution of income would result in a straight diagonal line, while a curved line signifies inequality. The further the curve deviates from the diagonal, the greater the income disparity. By analyzing the shape of the curve, policymakers and economists can gauge the extent of inequality in a society. The Lorenz curve provides valuable insights into wealth distribution, allowing for targeted interventions that address disparities and promote economic justice. Its interpretation is pivotal in formulating equitable policies.
Table of Contents
- Construction of the Lorenz curve
- Gini coefficient and its relation to the Lorenz curve
- Interpreting the Lorenz curve
- Limitations and criticisms of the Lorenz curve.
- Meaning of the Lorenz curve
(Gini Coefficient and Lorenz Curve)
Interpreting the Lorenz curve can help us understand income inequality within a country. This curve, named after economist Max Lorenz, visually represents the distribution of income among a population. By plotting the cumulative share of income against the cumulative share of the population, we can identify disparities in wealth.
A perfectly equal society would exhibit a straight diagonal line on the Lorenz curve, indicating that each segment of the population holds an equal share of the income. However, in reality, the curve typically deviates from this ideal line.
The further the curve bows away from the diagonal, the greater the income inequality. A more pronounced arch suggests that a small portion of the population possesses a large proportion of the income, while the majority receives a smaller share. Conversely, a flatter curve indicates a more equitable distribution, with income more evenly spread across society.
Additionally, the Lorenz curve allows us to calculate a statistic called the Gini coefficient. This value, derived from the area between the Lorenz curve and the ideal line, ranges from 0 to 1. A Gini coefficient of 0 represents perfect equality, while 1 represents extreme inequality.
Understanding the Lorenz curve and Gini coefficient is crucial for policymakers and researchers alike. It provides a tangible measure of income inequality and helps identify regions or groups that may require targeted interventions.
In conclusion, the Lorenz curve is a valuable tool for interpreting income inequality. By visually representing the distribution of income, it enables us to analyze and address disparities within a society.
Construction of the Lorenz curve
Construction of the Lorenz curve involves plotting the cumulative percentage of income or wealth against the cumulative percentage of the population. It is a graphical representation that helps us understand income inequality within a society. The curve is named after Max O. Lorenz, an American economist who introduced it in 1905.
To construct the Lorenz curve, we need data on the distribution of income or wealth in a given population. First, we arrange individuals or households from the poorest to the richest. Then, we calculate the cumulative percentage of income or wealth for each group. For example, if the bottom 20% of the population earns 5% of the total income, we mark that point on the graph.
Next, we calculate the cumulative percentage of the population. If the bottom 20% of the population consists of 10% of the total population, we mark that point on the graph. We repeat this process for each percentile, creating a series of points that connect to form the Lorenz curve.
The Lorenz curve provides a visual representation of income or wealth inequality. The closer the curve is to the diagonal line, the more equal the distribution. If the curve bows away from the diagonal line, it indicates greater inequality.
The Lorenz curve also allows us to calculate a summary statistic called the Gini coefficient. This coefficient measures the extent of inequality in a society. It is calculated as the area between the Lorenz curve and the diagonal line, divided by the total area under the diagonal line. The Gini coefficient ranges from 0 to 1, where 0 indicates perfect equality and 1 indicates perfect inequality.
Interpreting the Lorenz curve and the Gini coefficient helps policymakers and researchers understand the distributional implications of different policies. It provides insights into the impact of income redistribution programs, tax policies, and other interventions aimed at reducing inequality.
In conclusion, the construction of the Lorenz curve is a valuable tool in understanding income and wealth inequality within a society. By plotting cumulative percentages, we can visualize the distribution and measure its extent using the Gini coefficient. This information is crucial for policymakers and researchers seeking to address issues of inequality and promote more equitable societies.
Gini coefficient and its relation to the Lorenz curve
The Gini coefficient is a statistical measure used to quantitatively assess income inequality within a specific population. It is closely related to the Lorenz curve, which visually represents income distribution. By examining the Gini coefficient and the Lorenz curve together, policymakers and economists can gain a comprehensive understanding of wealth disparities and their implications.
The Gini coefficient ranges from 0 to 1, with 0 representing perfect equality, where every member of society has an equal share of wealth, and 1 representing extreme inequality, where one individual possesses all the wealth. This coefficient encapsulates the distribution of income across the entire population, providing a single value that summarizes the level of inequality.
The Lorenz curve, on the other hand, is a graphical representation of income distribution. It plots the cumulative percentage of total income received by individuals against the cumulative percentage of the population ranked by income. This curve visually illustrates the concentration of wealth and allows for a more intuitive understanding of income inequality.
The relationship between the Gini coefficient and the Lorenz curve is straightforward. The Gini coefficient is derived from the Lorenz curve by calculating the ratio of the area between the Lorenz curve and the line of perfect equality to the total area under the line of perfect equality.
A Gini coefficient closer to 0 indicates a more equal distribution of income, while a coefficient closer to 1 signifies a higher level of inequality. The shape of the Lorenz curve complements the Gini coefficient, providing a visual representation of income distribution that can reveal specific patterns and trends.
Understanding the Gini coefficient and the Lorenz curve is crucial for policymakers as they strive to address income inequality. By monitoring changes in the Gini coefficient and observing shifts in the shape of the Lorenz curve over time, policymakers can evaluate the effectiveness of policies aimed at reducing inequality.
In conclusion, the Gini coefficient and the Lorenz curve are valuable tools for comprehending income inequality. While the Gini coefficient provides a numerical representation, the Lorenz curve offers a visual depiction of income distribution. By analyzing these measures together, policymakers can gain valuable insights into the distribution of wealth and formulate effective policies to promote a more equitable society.
Interpreting the Lorenz curve
The Lorenz curve is a graphical representation that helps us understand income inequality in a given society. It measures the distribution of income among individuals and allows us to compare how evenly or unevenly income is distributed.
To interpret the Lorenz curve, we need to understand its shape. It is a line that starts at the bottom left corner of the graph and ends at the top right corner. The line represents the cumulative share of income held by the population, from poorest to richest. If the population had equal income, the Lorenz curve would be a straight line at a 45-degree angle.
However, in reality, income distribution is usually unequal. The more the Lorenz curve deviates from the 45-degree line, the greater the income inequality. The greater the curvature or bending of the line, the more severe the inequality.
One way to interpret the Lorenz curve is by looking at the Gini coefficient. This is a numerical measure derived from the Lorenz curve that ranges from 0 to 1. A Gini coefficient of 0 indicates perfect equality, where everyone has the same income. A Gini coefficient of 1 indicates extreme inequality, where one individual has all the income and the rest have none.
Another way to interpret the Lorenz curve is by comparing it to other curves representing different societies or time periods. By doing so, we can assess changes in income distribution over time or across countries.
It is important to note that the Lorenz curve does not tell us why income inequality exists or what causes it. It is simply a tool to visualize and measure inequality. The factors contributing to income inequality can be complex and multifaceted, including factors such as economic policies, education, and social dynamics.
In conclusion, the Lorenz curve is a powerful tool for interpreting income inequality. By analyzing its shape and comparing it to other curves, we can gain insights into the distribution of income in a society. However, it is crucial to remember that the Lorenz curve alone does not provide explanations for income inequality. Understanding the underlying causes requires further analysis and examination of various socioeconomic factors.
Limitations and criticisms of the Lorenz curve.
The Lorenz curve is a powerful tool for analyzing income inequality, but it is not without its limitations and criticisms. Understanding these limitations is crucial for a nuanced interpretation of the curve’s insights.
One limitation is that the Lorenz curve only captures inequality of income distribution without considering other important factors such as education, healthcare, and social mobility. These factors can greatly impact the well-being and quality of life of individuals, rendering the Lorenz curve alone insufficient for a comprehensive analysis of inequality.
Another criticism is that the Lorenz curve is based on aggregate data and may not accurately represent the experiences of specific individuals or groups within a society. It fails to consider differences in income distribution within different populations, making it less effective for understanding inequality among subgroups.
Furthermore, the Lorenz curve assumes that the distribution of income follows a specific mathematical shape, typically the Gini coefficient. Yet, this assumption may not hold true in all cases, as income distributions can vary significantly across different countries and time periods.
Additionally, the Lorenz curve does not account for non-monetary aspects of inequality, such as access to education, healthcare, and opportunities. These dimensions are crucial in understanding the full extent of inequality in a society, but they are not adequately reflected in the Lorenz curve.
Critics also argue that the Lorenz curve ignores the role of economic and social policies in shaping income inequality. Factors such as taxation, welfare programs, and labor market regulations can have significant effects on the distribution of income, yet they are not explicitly accounted for in the Lorenz curve.
Despite these limitations and criticisms, the Lorenz curve remains a valuable tool for visualizing income inequality and initiating discussions about distributional justice. Its simplicity and intuitive nature make it accessible to a wide range of audiences, and it serves as a starting point for further analysis and policy debates.
In conclusion, while the Lorenz curve provides a useful snapshot of income inequality, it is not without its limitations and criticisms. Understanding these limitations is essential for a comprehensive interpretation of the curve’s insights and for a more holistic understanding of inequality in society.
Meaning of the Lorenz curve
The Lorenz curve is a graphical representation of the distribution of income or wealth within a population. It was developed by American economist Max O. Lorenz in 1905 and is widely used to understand and analyze income inequality.
The curve is created by plotting the cumulative percentage of a population’s income on the y-axis against the cumulative percentage of the population on the x-axis. The resulting curve shows the degree of income concentration within the population. A perfectly equal distribution of income would result in a diagonal line, whereas a highly unequal distribution would result in a curve that deviates significantly from the diagonal.
The Lorenz curve is often used in conjunction with the Gini coefficient, which is a summary measure of income inequality derived from the curve. The Gini coefficient is calculated as the area between the Lorenz curve and the diagonal line, divided by the total area under the diagonal line. The coefficient ranges from 0 to 1, with 0 representing perfect equality and 1 representing extreme inequality.
Interpreting the Lorenz curve can provide valuable insights into the distribution of resources within a society. It can help policymakers and economists understand the impact of economic policies on income distribution and assess the effectiveness of social programs aimed at reducing inequality.
For example, a country with a steep Lorenz curve and high Gini coefficient indicates a significant concentration of wealth among a small portion of the population, suggesting a higher level of income inequality. This may necessitate policy interventions such as progressive taxation or targeted social welfare programs to redistribute wealth and promote a more equitable society.
On the other hand, a flatter Lorenz curve and lower Gini coefficient suggest a more equal distribution of income, indicating a fairer society with reduced income disparities. Governments in such countries may adopt policies that prioritize income mobility and equal opportunities for all citizens.
Understanding the meaning of the Lorenz curve is essential for policymakers, economists, and researchers concerned with income inequality. By analyzing the curve’s shape and the accompanying Gini coefficient, it becomes possible to assess the extent of inequality and devise appropriate measures to promote a more balanced distribution of resources within society. Ultimately, the goal is to create a society where everyone has the opportunity to thrive and reach their full potential, regardless of their socioeconomic background.