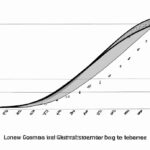
The Lorenz curve is a graphical representation that helps analyze income distribution within a given population. By plotting the cumulative percentage of income received by individuals against the cumulative percentage of the population, the curve provides insights into economic inequality. The closer the Lorenz curve is to the diagonal line of perfect equality, the fairer the income distribution. However, if the curve deviates significantly from the diagonal, it indicates inequality, with a larger area between the curve and the line representing a higher level of disparity. Understanding and interpreting the Lorenz curve is crucial in studying social and economic policies aimed at reducing income inequality.
(#31, Lorenz Curve)
The Lorenz curve is a graphical representation of income or wealth distribution within a society. It provides valuable insights into the level of inequality in a given population. The curve is named after Max O. Lorenz, an American economist who developed this tool in 1905. Interpreting the Lorenz curve involves analyzing its shape and comparing it to the line of perfect equality. The curve is plotted by cumulating the percentage of total income or wealth on the y-axis against the corresponding percentage of the population on the x-axis. The curve starts at the origin and slopes upwards, depicting the cumulative percentage of income or wealth owned by the population. The closer the Lorenz curve lies to the line of equality, the more equal the income or wealth distribution is within the population. On the other hand, a significant deviation from the line of equality indicates a higher level of inequality. The greater the distance between the Lorenz curve and the line of equality, the more unequal the distribution of income or wealth in society. Additionally, a commonly used summary statistic derived from the Lorenz curve is the Gini coefficient. The Gini coefficient measures income or wealth inequality on a scale from 0 to 1, with 0 representing perfect equality and 1 representing maximum inequality. A larger Gini coefficient implies greater inequality, while smaller values indicate a more equitable distribution. The interpretation of the Lorenz curve and Gini coefficient is essential for policymakers, economists, and social scientists as it helps identify the concentration of income or wealth and assists in designing appropriate policies to address inequality. By understanding the shape and slope of the Lorenz curve, policymakers can make informed decisions to promote fairness and social stability within a society.Construction of Lorenz curve
Construction of Lorenz Curve: The Lorenz curve is a graphical representation used in the field of economics to analyze income or wealth distribution within a population. It visually depicts the inequality of income or wealth by plotting cumulative percentages of the population against cumulative percentages of income or wealth. The construction process of a Lorenz curve involves the following steps: 1. Data Collection: To construct a Lorenz curve, data on the income or wealth distribution of a population is required. This data should provide information on the share of total income or wealth held by different segments of the population. 2. Calculation of Cumulative Percentages: The next step involves calculating the cumulative percentages of income or wealth and the cumulative percentages of the population. This is done by summing up the percentages for each segment of the population, starting from the lowest to the highest. 3. Ordering the Data: Once the cumulative percentages are calculated, the data is arranged in ascending order according to the income or wealth levels. This ordering is necessary to create accurate representations of the income or wealth distribution. 4. Plotting the Graph: With the ordered data, a graph can be plotted with the cumulative percentages of the population on the x-axis and the cumulative percentages of income or wealth on the y-axis. The resulting curve represents the Lorenz curve. 5. Perfect Equality Line: In a perfectly equal distribution of income or wealth, the Lorenz curve would coincide with a diagonal line. This line is called the perfect equality line and represents a situation where each segment of the population has an equal share of income or wealth. 6. Gini Coefficient Calculation: The Lorenz curve is also associated with the calculation of the Gini coefficient, which is a numerical measure of income or wealth inequality. The Gini coefficient is derived from the area between the Lorenz curve and the perfect equality line. The closer the Lorenz curve is to the perfect equality line, the lower the Gini coefficient and thus lower inequality. 7. Interpreting the Curve: The shape of the Lorenz curve provides insights into the income or wealth distribution in a population. A steep curve indicates higher inequality, with a larger share of income or wealth concentrated among a smaller proportion of the population. A flatter curve indicates less inequality, with a more equal distribution. In conclusion, the construction of a Lorenz curve involves gathering data on income or wealth distribution, calculating cumulative percentages, ordering the data, plotting the graph, and analyzing the shape of the curve. This curve and the associated Gini coefficient provide valuable insights into the inequality within a population, making them essential tools for economists studying income or wealth disparities.
Definition of Lorenz curve
The Lorenz curve is a graphical representation that measures income or wealth inequality within a given population. Developed by economist Max O. Lorenz in 1905, this curve provides insights into the distribution of a country’s resources among its citizens. It visually depicts the cumulative percentage of the total income or wealth held by a specific percentage of the population. The horizontal axis of the Lorenz curve represents the cumulative percentage of the population, starting with the lowest earner and progressing to the highest earner. Meanwhile, the vertical axis illustrates the cumulative percentage of the total income or wealth held by this portion of the population. Ideally, if a country has perfect income equality, the Lorenz curve will be a straight diagonal line. However, in reality, the Lorenz curve usually exhibits a concave shape, indicating income or wealth inequality. The greater the curvature of the curve, the higher the level of inequality present in the society. The Gini coefficient, a numerical measure derived from the Lorenz curve, quantifies this inequality by calculating the area between the Lorenz curve and the diagonal line of perfect equality. A Gini coefficient of 0 represents complete equality, while a coefficient of 1 signifies maximum inequality. The Lorenz curve and Gini coefficient are essential tools for analyzing income or wealth distribution patterns for various purposes. Governments and policymakers use this information to design and implement effective social policies, aiming to reduce economic disparities and promote fairness. Economists and researchers employ the Lorenz curve to understand the socioeconomic conditions of a nation, compare different countries, and evaluate the effectiveness of various economic policies. Interpreting the Lorenz curve involves examining its shape, curvature, and proximity to the diagonal line of perfect equality. The curve’s proximity to the diagonal line indicates the level of income or wealth equality in the society. A curve that closely resembles the diagonal line reveals a fair distribution, while a curve lying far from the diagonal indicates significant inequality. Furthermore, the steepness of the curve demonstrates the concentration of income or wealth within specific segments of the population. A steeper curve implies greater concentration, suggesting that a small portion of the population controls a significant percentage of the country’s resources. Conversely, a flatter curve signifies a more even distribution, with a larger percentage of the population sharing the wealth. In conclusion, the Lorenz curve is a graphical representation that showcases income or wealth inequality. It offers a visual understanding of a country’s resource distribution among its citizens. By analyzing the shape, curvature, and proximity of the Lorenz curve, policymakers, economists, and researchers can gain valuable insights into the level of inequality within a society and take appropriate actions to address it.
Interpretation of Lorenz curve
The Lorenz curve is a graphical representation that is commonly used in economics to analyze income distribution within a population. It provides a visual depiction of the inequality or fairness of income distribution. Here is some information to help you understand and interpret the Lorenz curve: 1. Construction of the Lorenz Curve: The Lorenz curve is constructed by plotting the cumulative percentage of the population on the x-axis and the cumulative percentage of total income on the y-axis. The data used for constructing the curve includes income or wealth distribution for a particular population. 2. Perfect Equality Line: The curve starts at the origin (0,0) and ends at the point (1,1). The diagonal line from the origin to the endpoint represents perfect equality, where every person within the population has an equal share of income or wealth. 3. Curvature of the Lorenz Curve: The shape of the Lorenz curve provides insights into the degree of income or wealth inequality within a population. If the curve lies closer to the perfect equality line, it indicates a fairer distribution, with less inequality. Conversely, if the curve deviates further from the perfect equality line, it signifies a higher level of inequality. 4. Gini Coefficient: The Gini coefficient is a numerical measure derived from the Lorenz curve that quantifies income or wealth inequality. It ranges from 0 to 1, with 0 representing perfect equality and 1 indicating maximum inequality. The Gini coefficient is calculated by dividing the area between the Lorenz curve and the perfect equality line by the total area below the perfect equality line. 5. Area between the Lorenz Curve and the Perfect Equality Line: The area between the Lorenz curve and the perfect equality line represents the extent of inequality within the population. A larger area signifies a greater level of inequality, whereas a smaller area suggests a more equal distribution of income or wealth. 6. Interpreting Changes in the Lorenz Curve: Comparing different Lorenz curves over time allows for the analysis of changes in income or wealth inequality within a population. If a later Lorenz curve lies below an earlier one, it indicates progress towards a more equal distribution. Conversely, if the later curve lies above the earlier one, it suggests an increase in inequality. 7. Policy Implications: The interpretation of the Lorenz curve has significant policy implications. Governments and policymakers can use the data obtained from the Lorenz curve to develop strategies aimed at reducing inequality, such as implementing progressive taxation, increasing access to education and healthcare, or creating social welfare programs. In conclusion, the Lorenz curve is a useful tool for interpreting and visualizing income or wealth inequality within a population. Understanding the shape and position of the curve, as well as the associated Gini coefficient, helps researchers and policymakers gauge the level of inequality and develop appropriate measures to address it.
Limitations of Lorenz curve.
The Lorenz curve is a graphical representation used in economics to illustrate income distribution within a society. While it is a useful tool for understanding inequality, it is important to recognize its limitations in order to interpret it accurately. Here are some key limitations of the Lorenz curve: 1. Oversimplification: The Lorenz curve assumes that income distribution can be accurately represented on a two-dimensional graph. However, in reality, income inequality is a complex and multi-dimensional issue affected by various factors such as education, race, gender, and social mobility. Therefore, relying solely on the Lorenz curve can oversimplify the complexity of inequality. 2. Lack of contextual information: The Lorenz curve does not provide any information about the sources of income or the underlying causes of inequality. It only focuses on the distribution of income and does not consider factors such as the level of economic development, government policies, or historical context. To fully understand inequality, it is necessary to consider these contextual factors alongside the Lorenz curve. 3. Inability to capture non-monetary well-being: The Lorenz curve is solely based on income distribution, which does not necessarily reflect overall well-being or quality of life. It does not account for aspects such as access to healthcare, education, or basic needs, which are vital for assessing inequality comprehensively. Therefore, using the Lorenz curve alone may lead to an incomplete understanding of the societal dynamics related to inequality. 4. Susceptibility to manipulation: The Lorenz curve is based on self-reported income data, which may be subject to manipulation or inaccuracies. In societies where income disparities are pronounced, individuals may have incentives to underreport or hide their income, leading to an inaccurate representation of inequality. Additionally, the use of pre-tax income data may overlook the impact of taxation policies on income distribution. 5. Limited time frame: The Lorenz curve typically represents income distribution at a particular point in time. It does not capture changes or trends over time, making it difficult to track shifts in inequality dynamics. To gain a more nuanced understanding of inequality, it is important to complement the Lorenz curve with longitudinal data and analysis. Overall, the Lorenz curve serves as a valuable visualization tool for understanding income distribution within a society. However, it is crucial to consider its limitations and to complement its use with additional data and analysis to foster a more comprehensive understanding of inequality.
Uses of Lorenz curve
The Lorenz curve is a graphical representation used in the field of economics to analyze income and wealth distribution within a population. It plots the cumulative proportion of total income or wealth received by the cumulative proportion of the population. The Lorenz curve provides valuable insights into the level of inequality present in a society and is widely used for various purposes. Here are some key uses of the Lorenz curve: 1. Measuring Inequality: The primary use of the Lorenz curve is to measure and compare inequality across different societies or time periods. By comparing the shape and position of multiple Lorenz curves, economists can determine whether income or wealth distribution has become more or less unequal over a given period. This helps policymakers evaluate the effectiveness of social and economic policies aimed at reducing inequality. 2. Poverty Analysis: The Lorenz curve is also employed to assess the extent of poverty within a population. By comparing the curve with a diagonal reference line (known as the Line of Perfect Equality), analysts can estimate the number or percentage of individuals below a certain income threshold. This information is crucial for designing poverty reduction programs and targeting social protection measures effectively. 3. Policy Evaluation: Governments and organizations use the Lorenz curve to evaluate the impact of various policies on income distribution. By comparing the actual Lorenz curve with the predicted curve under different policy scenarios, policymakers can understand how different policy options might affect inequality. This analysis helps in making informed decisions about taxation, redistribution, and targeted interventions to address inequality effectively. 4. International Comparisons: The Lorenz curve can be used for comparisons of income or wealth distribution across countries. By examining the Lorenz curves of different nations, economists gain insights into the disparities and differences in economic structures, social policies, and development levels. This information is valuable for identifying best practices and strategies for reducing inequality globally. 5. Economic Development: The Lorenz curve provides a visual representation of income distribution patterns, making it a powerful tool for assessing the overall economic development of a country. By analyzing changes in the Lorenz curve over time, economists can understand how economic growth affects income distribution. This information helps policymakers design development strategies that aim to ensure that the benefits of growth are spread more equitably. In summary, the Lorenz curve is widely used in economic analysis as a tool for measuring and evaluating income and wealth distribution. Its uses extend to measuring inequality, analyzing poverty, evaluating policies, comparing nations, and assessing economic development. By employing the Lorenz curve, researchers and policymakers can gain valuable insights that aid in understanding and addressing issues of inequality in society.