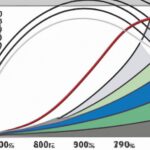
The Lorenz curve is a powerful tool used in economics to visualize income distribution. However, it comes with assumptions and limitations. First, it assumes a closed economy, ignoring international income disparities. Second, it assumes that income is the only measure of well-being, disregarding other factors like education and healthcare. Third, it assumes that the distribution of income is static over time, neglecting any changes that might occur. Additionally, the Lorenz curve cannot capture the complex dynamics of an economy, such as the effects of economic policies or technological advancements. Despite these limitations, the Lorenz curve remains a valuable tool for understanding income inequality and informing policy decisions.
Table of Contents
- Assumption of continuous income distribution
- Assumption of perfect equality
- Assumption of ranked distribution
- Limitations of Lorenz curve.
- Types of assumptions in Lorenz curve
(Gini Coefficient and Lorenz Curve)
Assumptions and limitations are inherent in the use of the Lorenz curve, a tool often used to analyze income distribution. It is crucial to understand these factors to interpret the results accurately.
One assumption is that the distribution is based on income alone, neglecting other indicators of wealth like assets or education. Another assumption is that individuals are classified into homogeneous groups, ignoring the diverse characteristics within each group.
Additionally, the Lorenz curve assumes that there is no income underreporting or evasion, which may skew the results. It also disregards the impact of government policies and social welfare programs that can influence income distribution.
Moreover, the Lorenz curve is limited in its ability to capture changes in income distribution over time. It provides a static snapshot, but fails to depict dynamics or trends. It does not account for factors like economic growth or changes in population size, which can significantly affect income distribution.
Furthermore, the Lorenz curve is sensitive to the size and number of income categories used. Small variations in these categories can lead to different results, making comparisons challenging.
Despite these assumptions and limitations, the Lorenz curve remains a valuable tool for understanding income inequality. It offers insights into the concentration of income and helps policymakers formulate strategies to address inequality. However, it is crucial to consider these limitations and complement the analysis with other measures to gain a comprehensive understanding of income distribution.
Assumption of continuous income distribution
Assumption of continuous income distribution is one of the key assumptions underlying the concept of the Lorenz curve. This assumption suggests that income is evenly distributed across the population, with no extreme outliers or disparities.
The assumption of continuous income distribution is important because it allows for a simplified analysis of income inequality. By assuming that income follows a smooth distribution, the Lorenz curve can provide a visual representation of how income is distributed across a population.
However, it is important to note that the assumption of continuous income distribution may not always hold true in real-world scenarios. In reality, income distribution is often skewed, with a small percentage of individuals holding a disproportionately large share of the total income.
Despite this limitation, the assumption of continuous income distribution still provides valuable insights into income inequality. It allows policymakers and researchers to compare different populations and measure the extent of income disparities.
Moreover, the assumption of continuous income distribution does not imply that everyone has the same level of income. Rather, it suggests that the distribution of income follows a smooth curve, without any sudden jumps or discontinuities.
The assumption of continuous income distribution is often used in conjunction with other assumptions to analyze income inequality. For example, the assumption of ordinal utility is commonly employed, which suggests that individuals can rank their preferences but not assign precise numerical values to them.
In conclusion, the assumption of continuous income distribution is an important assumption underlying the concept of the Lorenz curve. While it may not always hold true in practice, it provides a useful framework for analyzing income inequality. By understanding these assumptions and limitations, researchers and policymakers can gain valuable insights into the distribution of income in a given population.
Assumption of perfect equality
Assumption of perfect equality is a key aspect when evaluating the assumptions and limitations of the Lorenz curve. This assumption posits that all individuals within a society have equal access to resources and opportunities, leading to an equitable distribution of income or wealth.
However, in reality, perfect equality is rarely achieved in any society. This assumption fails to consider the existence of social, economic, and political factors that perpetuate inequality. Socioeconomic disparities, discrimination, and unequal access to education and healthcare all contribute to an uneven distribution of wealth and income.
The assumption of perfect equality is problematic because it overlooks the impact of privilege and systemic disadvantages. It fails to recognize the role of factors such as race, gender, and class in determining one’s economic standing. These inequalities create a disproportionate distribution of resources, resulting in a skewed representation when plotting the Lorenz curve.
Moreover, the assumption of perfect equality neglects the influence of external shocks and fluctuations in the economy. Economic recessions, financial crises, and other unforeseen events disrupt the equilibrium and can significantly impact income distribution. These fluctuations are not accounted for by the assumption, leading to a distorted representation of the Lorenz curve.
Another limitation of assuming perfect equality is that it disregards the concept of intergenerational transfers of wealth. Inheritance and family wealth can perpetuate inequality across generations, creating a disparity in income and wealth distribution. The assumption fails to account for these transfers, once again distorting the Lorenz curve.
In conclusion, the assumption of perfect equality within the Lorenz curve is a simplified view that does not accurately represent the complexities of income and wealth distribution. While it serves as a theoretical benchmark, it fails to consider the social, economic, and political factors that perpetuate inequality. Recognizing and addressing these limitations is important to gain a more nuanced understanding of income inequality and its impact on society.
Assumption of ranked distribution
Assumption of ranked distribution refers to the underlying belief that individuals can be ranked based on their economic status. This assumption is a key component of the Lorenz curve, which is a graphical representation of income inequality within a population.
In order to construct the Lorenz curve, it is necessary to have data that ranks individuals according to their income or wealth. This assumption assumes that it is possible to determine a person’s economic standing relative to others in the population. This ranking allows for the calculation of cumulative income shares to be plotted on the curve.
However, the assumption of ranked distribution is not without its limitations. One major limitation is that it simplifies the complexity of income inequality by reducing it to a single dimension. It assumes that economic well-being can be accurately captured and measured by a single variable such as income or wealth. This overlooks the multidimensional nature of inequality, including factors such as education, health, and social capital.
Another limitation is that the assumption of ranked distribution assumes that individuals can be neatly classified into discrete categories based on their economic status. In reality, economic status is not always clear-cut and can be subject to change over time. This assumption fails to capture the fluidity of social mobility and the fact that individuals can move up or down the income ladder.
Additionally, the assumption of ranked distribution assumes that there is a linear relationship between cumulative income shares and population size. This assumes that each increment in the population corresponds to a proportional increment in income shares. However, this may not always be the case, as the distribution of income can be shaped by various factors such as government policies, market forces, and historical contexts.
In conclusion, while the assumption of ranked distribution is a necessary component of the Lorenz curve, it is not without its limitations. It oversimplifies the complexity of income inequality, fails to capture the fluidity of social mobility, and assumes a linear relationship between cumulative income shares and population size. These limitations should be considered when interpreting the findings of the Lorenz curve and understanding the dynamics of income inequality within a population.
Limitations of Lorenz curve.
The Lorenz curve, a graphical representation of income inequality, has its limitations. One limitation is its reliance on the assumption of perfect income distribution, which may not reflect the reality of the world. Incomparable economies, such as those with varied industries or social welfare policies, may render the Lorenz curve less effective in measuring inequality accurately.
Another limitation lies in its inability to account for non-monetary factors. Income is just one aspect of inequality, with factors like education, healthcare access, and socio-political power playing crucial roles. The Lorenz curve fails to capture these dimensions, making it an incomplete tool for assessing overall inequality.
Additionally, the Lorenz curve assumes that the total population is represented on the horizontal axis. However, this assumption neglects factors like age disparities and unequal representation, leading to distortion in the measurement of inequality.
Furthermore, the Lorenz curve does not reflect changes over time. It provides a snapshot of inequality at a specific point, but fails to account for any shifts in income distribution. Changes in economic policies or demographic trends may render the Lorenz curve less useful in capturing the dynamics of inequality.
Moreover, the Lorenz curve may not accurately represent inequality within smaller groups. It assumes homogeneity within the total population, disregarding the potential disparities that exist within subgroups.
Another limitation of the Lorenz curve is its inability to capture the psychological impact of inequality. While the curve provides a quantitative measure of income distribution, it fails to measure the emotional and social consequences of inequality on individuals and communities. This limitation underscores the need for a more comprehensive approach to understanding and addressing inequality.
In conclusion, while the Lorenz curve is a useful tool for visualizing income inequality, it has several limitations. Its reliance on assumptions of perfect income distribution, its inability to account for non-monetary factors, its assumption of representative populations, its static nature, its limited scope within subgroups, and its failure to capture the psychological impact of inequality all contribute to its limitations. Recognizing these constraints is essential for a more nuanced understanding of inequality and for developing effective policies to address it.
Types of assumptions in Lorenz curve
Types of assumptions in Lorenz Curve
The Lorenz curve is a graphical representation of income inequality within a population. It is a useful tool for economists and policymakers to understand the income distribution and make informed decisions. However, it is important to be aware of the assumptions underlying the Lorenz curve analysis.
Firstly, one assumption is that income is the only measure of inequality. While income is a commonly used metric, it does not capture other dimensions of inequality, such as wealth or access to resources. It is essential to consider a broader range of factors to get a comprehensive understanding of inequality.
Secondly, the Lorenz curve assumes that individuals have the same preferences and opportunities. However, in reality, people have diverse tastes, abilities, and opportunities, which can affect their income levels. Failure to account for these differences may lead to an oversimplification of inequality.
Another assumption is that the Lorenz curve is based on a snapshot of income data at a specific point in time. However, income inequality is dynamic and can change over time. Changes in economic policies, technological advancements, or other factors can significantly impact income distribution. Therefore, it is crucial to analyze income inequality trends over time rather than relying solely on one-time data.
Furthermore, the Lorenz curve assumes that all individuals accurately report their income. However, underreporting or misreporting of income can distort the accuracy of the curve. Non-monetary income such as in-kind benefits or hidden income may not be fully captured, leading to an incomplete depiction of inequality.
Lastly, the Lorenz curve assumes that the population is homogeneous in terms of household size and composition. However, household size and composition can influence income distribution. For example, households with more members may have economies of scale, resulting in lower per capita income. Therefore, it is important to consider household characteristics when interpreting the Lorenz curve.
Understanding these assumptions is crucial for interpreting the Lorenz curve accurately. While the Lorenz curve provides valuable insights into income inequality, it is essential to complement it with other measures and consider the shortcomings of these assumptions. By doing so, policymakers can develop more comprehensive and targeted strategies to tackle inequality effectively.
In conclusion, the Lorenz curve is a useful tool for analyzing income inequality. However, it is important to be mindful of the assumptions underlying its analysis. Recognizing the limitations of the Lorenz curve can help in developing a more nuanced understanding of inequality, leading to more effective policies and interventions.