The Gini coefficient is a measure of income inequality that helps policymakers understand the distribution of wealth within a population. Assumptions and interpretations of the Gini coefficient are crucial for making informed decisions. One assumption is that inequality is a relevant concern, as the coefficient reflects disparities in income. Another assumption is that the Gini coefficient accurately captures the degree of inequality, as it considers the entire income distribution. Interpretations of the coefficient vary, with some arguing that a higher coefficient indicates greater inequality, while others believe it represents economic efficiency. Understanding these assumptions and interpretations is vital for policymakers aiming to address income inequality and promote a more equitable society.
Table of Contents
- Alternative measures of income inequality
- Application of the Gini Coefficient in different countries
- Calculation method of the Gini Coefficient
- History of the Gini Coefficient
- Limitations of the Gini Coefficient
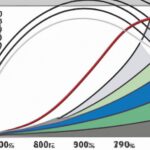
(Gini Coefficient and Lorenz Curve)
Assumptions and interpretations of Gini coefficient shape our understanding of wealth distribution within a society. Gini coefficient, a statistical measure developed by Italian statistician Corrado Gini, quantifies income inequality. It ranges from 0 to 1, where 0 represents perfect equality, and 1 indicates extreme inequality.
One assumption is that the Gini coefficient assumes a bell curve distribution of income. It implies that most people fall within the middle-income range, with fewer at the extremes. However, this assumption may not hold true in societies with a significant wealth gap, where income is concentrated in the hands of a few.
Another assumption is that the Gini coefficient focuses solely on income inequality and does not account for other aspects of wellbeing, such as access to education, healthcare, or social services. Therefore, it captures only a limited perspective of inequality.
Interpreting the Gini coefficient requires understanding its implications. A higher coefficient reflects greater income inequality, while a lower coefficient suggests more equitable income distribution. However, interpreting the coefficient in isolation can be misleading, as it does not provide insight into the causes or consequences of inequality.
Moreover, the Gini coefficient assumes that income distribution is independent of population size. However, it fails to capture the dynamics of population growth or decline, which can influence income distribution patterns.
In conclusion, the Gini coefficient offers a quantitative measurement of income inequality, but it is important to recognize its assumptions and limitations. It provides valuable insights into wealth distribution within a society, but should be used in conjunction with other indicators to gain a comprehensive understanding of inequality and its impacts.
Alternative measures of income inequality
Alternative measures of income inequality provide a fresh perspective on the distribution of wealth within a society. While the Gini coefficient is a widely used tool to assess income inequality, it has its limitations. These alternative measures aim to address those limitations and provide a more comprehensive understanding of the income gap.
One such alternative measure is the Palma ratio, which compares the income share of the richest 10% to the poorest 40%. By focusing on these extreme ends of the income distribution, the Palma ratio highlights the concentration of wealth in the hands of a few.
Another alternative measure is the Hoover index, which examines income inequality by measuring the gap between the Lorenz curve and the line of perfect equality. It takes into account both the concentration of wealth in the higher income groups and the dispersion of wealth in the lower income groups.
The Atkinson index is yet another alternative measure that takes into account society’s aversion to inequality. It incorporates a social welfare function that reflects the diminishing marginal utility of income, meaning that a dollar has a greater impact on well-being for someone with lower income than for someone with higher income.
A fourth alternative measure is the coefficient of variation, which represents the standard deviation of income divided by the mean income. This measure captures the degree of income variability within a society, providing insight into the stability and volatility of income distribution.
Each of these alternative measures offers a unique perspective on income inequality and complements the Gini coefficient. By considering multiple measures, policymakers and researchers can gain a more nuanced understanding of the income gap and make more informed decisions to address inequalities.
It is important to note that no single measure can capture the complexity and multidimensionality of income inequality. However, by utilizing a combination of measures, we can paint a clearer picture of the distribution of wealth and develop more effective strategies for reducing inequality.
In conclusion, alternative measures of income inequality provide valuable insights into the distribution of wealth within a society. By considering a range of measures, policymakers and researchers can gain a more comprehensive understanding of income inequality and develop targeted strategies to promote a more equitable society. It is imperative that we continue to explore and refine these measures to ensure a fair and just distribution of resources.
Application of the Gini Coefficient in different countries
The Gini coefficient is a widely used measure of income inequality that provides insights into the distribution of wealth within a country. It is calculated on a scale of 0 to 1, where 0 represents perfect equality and 1 represents extreme inequality. The application of the Gini coefficient in different countries allows for comparisons that can shed light on the disparities within and between nations.
In developed countries like Sweden, the Gini coefficient tends to be lower, indicating a more equal distribution of income. This is largely attributed to progressive taxation policies, robust social welfare systems, and investment in education and healthcare. As a result, Sweden has one of the smallest income gaps in the world.
On the other end of the spectrum, countries like South Africa and Brazil often have high Gini coefficients, indicating significant income inequality. These countries face challenges such as a history of racial inequality, limited access to education and job opportunities, and inadequate social welfare systems. Efforts are being made in these countries to address these issues and reduce income disparities.
In emerging economies like China and India, the Gini coefficient has been rising over the years. Rapid economic growth has led to a concentration of wealth in the hands of a few, contributing to higher levels of inequality. This has spurred governments to implement policies aimed at reducing income disparities and promoting inclusive growth.
In some countries, such as the United States, the Gini coefficient has also been on the rise. Factors such as technological advancements, globalization, and decreasing labor union membership have contributed to widening income gaps. This has sparked debates on the need for policy interventions to promote more equitable wealth distribution.
It is essential to interpret the Gini coefficient in the context of each country’s unique socio-economic factors. While the coefficient provides valuable insights into income inequality, it does not capture other dimensions of wellbeing, such as access to healthcare, education, and social mobility. Therefore, it is crucial to consider complementary indicators and comprehensive policies to address the complexities of inequality.
In conclusion, the application of the Gini coefficient in different countries allows policymakers, researchers, and citizens to understand the extent of income inequality and its underlying causes. By analyzing these disparities, governments can design targeted policies to promote a more equitable distribution of wealth and opportunities, ultimately contributing to sustainable development and social cohesion.
Calculation method of the Gini Coefficient
The calculation method of the Gini Coefficient is a mathematical tool used to measure income inequality within a population. It is a widely accepted measure that provides valuable insights into the distribution of wealth or income across different socio-economic groups. The Gini Coefficient ranges from 0 to 1, with 0 representing perfect equality, where everyone has the same income, and 1 representing extreme inequality, where one individual has all the income and everyone else has none.
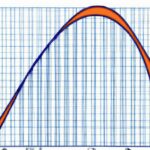
To calculate the Gini Coefficient, the first step is to organize the population in ascending order based on their income or wealth. Next, a Lorenz curve is constructed by plotting the cumulative percentage of the population on the x-axis and the cumulative percentage of income or wealth on the y-axis. The Lorenz curve represents the actual distribution of income or wealth in the population.
The Gini Coefficient is then derived by calculating the area between the Lorenz curve and the line of perfect equality (also known as the Lorenz curve of a hypothetical equitable distribution). This involves calculating the area between the Lorenz curve and the diagonal line that runs from the origin to the point of perfect income or wealth equality.
Mathematically, the Gini Coefficient can be expressed as the ratio of the area between the Lorenz curve and the line of perfect equality to the total area under the line of perfect equality. This can be simplified to the difference between the cumulative percentages of the population and income or wealth.
The Gini Coefficient can be interpreted as a single value that summarizes the degree of inequality within a population. A value close to 0 indicates a more equal distribution of income or wealth, while a value closer to 1 implies a greater degree of inequality.
It is important to note that the Gini Coefficient has its limitations. It gives a static snapshot of inequality at a specific point in time and does not capture changes over time. Additionally, it does not provide information on the underlying causes of income or wealth inequality, nor does it consider factors such as social mobility or access to opportunities.
In conclusion, the Gini Coefficient is a valuable tool for measuring income or wealth inequality. By understanding its calculation method and interpreting its results, policymakers and researchers can gain valuable insights into the distribution of resources within a population, helping to inform and shape more equitable policies and interventions.
History of the Gini Coefficient
The history of the Gini coefficient, a measure of income inequality, can be traced back to the early 20th century. It was developed by Italian economist Corrado Gini in 1912 as a way to quantify income distribution within a population.
Gini believed that understanding income inequality was crucial for economists and policymakers to make informed decisions about social welfare and economic development. His coefficient sought to provide a standardized measure that could be applied across different countries and time periods.
The Gini coefficient is based on the Lorenz curve, a graphical representation of income distribution. Gini’s formula calculates the area between the Lorenz curve and the line of perfect equality, which represents a society where everyone has the same income. The resulting value ranges from 0 to 1, with 0 indicating perfect equality and 1 indicating maximum inequality.
Initially, the Gini coefficient gained traction mainly in academic circles. It was used to analyze income inequality in different countries and compare trends over time. However, it wasn’t until the mid-20th century that the Gini coefficient started to gain popularity as a tool for policymakers.
In the 1960s and 1970s, governments and international organizations began to take notice of the Gini coefficient’s potential as a policy indicator. It provided a simple and straightforward way to measure income inequality and highlight potential social issues and disparities.
Since then, the Gini coefficient has been used in a variety of contexts, including analyzing income inequality in different regions, assessing the impact of government policies, and monitoring progress towards poverty reduction goals.
However, it is important to note that the Gini coefficient has its limitations. It only captures income distribution and does not take into account other important factors such as wealth or access to resources. Additionally, the Gini coefficient does not provide insights into the causes or consequences of income inequality.
Despite these limitations, the Gini coefficient remains a widely used and recognized measure of income inequality. Its historical development and ongoing use reflect the importance of understanding and addressing income disparities within societies. As policymakers continue to grapple with issues of inequality, the Gini coefficient continues to play a vital role in shaping discussions and informing policy decisions.
Limitations of the Gini Coefficient
The Gini coefficient is a widely used measure of inequality, but it has its limitations. One of the main limitations is that it only measures relative inequality, not absolute inequality. This means that it does not take into account the overall level of income or wealth in a society. For example, a society with high levels of inequality may still have a relatively low Gini coefficient if the overall level of income or wealth is also low.
Another limitation of the Gini coefficient is that it does not capture the full extent of inequality in a society. It is a single summary statistic that condenses the entire distribution of income or wealth into a single number. This means that it may miss important nuances and variations in the distribution. For example, it may not capture differences in inequality between different regions or demographic groups.
Additionally, the Gini coefficient assumes that all income or wealth is equally distributed within each income or wealth group. However, this assumption may not hold true in reality. There may be within-group inequality, where some individuals within a group have much higher incomes or wealth than others. This can lead to an underestimation of inequality by the Gini coefficient.
Furthermore, the Gini coefficient is sensitive to the choice of income or wealth groups used in its calculation. Different choices can produce different values, making it difficult to compare inequality between different studies or countries. This is known as the “grouping problem” and can introduce a significant amount of uncertainty into the measurement of inequality.
Lastly, the Gini coefficient does not capture other dimensions of inequality, such as educational or health disparities. It solely focuses on income or wealth inequality, neglecting other important aspects of social inequality. This means that it provides only a partial view of the overall level of inequality in a society.
In conclusion, while the Gini coefficient is a useful tool for measuring relative inequality, it has several limitations. It does not account for absolute inequality, may miss important variations in the distribution, assumes equal distribution within each group, is sensitive to grouping choices, and neglects other dimensions of inequality. Therefore, it is important to consider these limitations when interpreting and comparing Gini coefficients.