The Lorenz curve, while a useful tool for understanding income inequality, has its limitations. Firstly, it only focuses on income distribution and does not account for other socio-economic factors such as wealth, education, or access to public services. Additionally, the Lorenz curve assumes a homogenous population, disregarding variations within different segments of society. It also does not provide information on the causes or drivers of inequality, making it difficult to develop targeted policies for reducing inequality. Lastly, the curve can be misleading if the income distribution is highly skewed or if there are extreme outliers. These limitations highlight the need for complementary measures and a more holistic approach to understanding and addressing inequality.
(Gini's Coefficient: Measure of Inequality – Basis, Calculation, Advantages, Disadvantages)
The Lorenz Curve is a graphical representation of income or wealth distribution within a given population. While it is widely used and insightful, it also has some limitations that need to be considered. Firstly, the Lorenz Curve assumes that income or wealth distribution follows a cumulative distribution function. This assumption may not always hold true in reality, as there are various factors such as government policies, economic conditions, and social dynamics that can affect the distribution of income or wealth. Therefore, the curve may not accurately depict the true distribution pattern. Secondly, the Lorenz Curve is based on aggregated data, which can mask significant disparities within different segments of the population. It does not provide a detailed examination of the distribution pattern within specific subgroups, such as gender, ethnicity, or socioeconomic status. Consequently, it may fail to capture the full extent of inequality that exists within a society. Another limitation of the Lorenz Curve is that it does not consider non-monetary forms of inequality, such as access to education, healthcare, or social services. These factors can significantly impact an individual’s well-being and opportunities, and failing to account for them may paint an incomplete picture of inequality. Furthermore, the Lorenz Curve does not account for changes over time. It provides a snapshot of income or wealth distribution at a specific point in time, but it does not show how the distribution changes over periods of economic growth or decline. This limitation prevents a comprehensive understanding of the dynamics and trends in inequality within a society. Lastly, the Lorenz Curve assumes that individuals’ preferences for income or wealth distribution can be accurately represented by their actual income or wealth levels. However, people’s satisfaction or dissatisfaction with their own position relative to others may not align with their absolute income or wealth level. This psychological aspect is not adequately captured by the curve. In conclusion, while the Lorenz Curve is a useful tool for analyzing income or wealth distribution, its limitations should be duly recognized. It assumes a cumulative distribution function, relies on aggregated data, overlooks non-monetary forms of inequality, ignores changes over time, and fails to account for subjective perceptions of inequality. Understanding these limitations is essential for a comprehensive analysis of income or wealth distribution in any given population.Alternative measures and approaches to inequality analysis
Alternative measures and approaches to inequality analysis provide additional perspectives on assessing and understanding economic and social disparities. These measures and approaches go beyond the traditional Lorenz curve to offer a more comprehensive understanding of inequality. Here are several alternative measures and approaches to consider: 1. Gini coefficient: One commonly used alternative to the Lorenz curve is the Gini coefficient. It measures the extent to which the distribution of income or wealth deviates from perfect equality, ranging from 0 (perfect equality) to 1 (maximum inequality). The Gini coefficient provides a single summary measure and facilitates cross-country comparisons. 2. Theil index: The Theil index is another alternative measure that captures both within-group and between-group inequality. It considers how much of the total inequality is explained by inequalities within different subgroups. By accounting for both intra and intergroup disparities, the Theil index provides a more nuanced understanding of inequality. 3. Atkinson index: The Atkinson index focuses on the societal aversion to inequality, taking into account different levels of societal tolerance for income disparities. It allows for varying degrees of inequality aversion and provides a helpful tool for policymakers to gauge the impact of their redistributive efforts. 4. Multidimensional inequality: Instead of solely focusing on income or wealth disparities, a multidimensional approach considers a broader range of factors that contribute to inequality, such as health, education, and access to basic services. By exploring various dimensions simultaneously, this approach provides a more holistic view of inequality. 5. Capabilities approach: The capabilities approach, developed by economist Amartya Sen, emphasizes people’s freedoms and abilities to lead lives fulfilled with valuable opportunities. This approach goes beyond income measures and focuses on individuals’ capabilities to achieve well-being. It takes into account factors such as education, health, and social support, recognizing that inequality extends beyond material wealth. 6. Inequality of opportunity: Inequality of opportunity examines the impact of circumstances beyond individual control, such as gender, race, or socioeconomic background, on social and economic outcomes. By focusing on inequality that arises due to circumstances beyond an individual’s control, this approach highlights policy interventions to promote equality of opportunity for all. 7. Relative deprivation: This approach considers not only absolute income or material possessions but also the relative position of individuals within society. It sheds light on how individuals perceive their own position in comparison to others, allowing for a deeper understanding of the psychological and social implications of inequality. By incorporating these alternative measures and approaches to inequality analysis, policymakers and researchers can gain a more nuanced understanding of inequality and develop targeted strategies to address its underlying causes. These approaches help identify specific areas where interventions are needed and foster a more equitable society.
Assumptions and limitations of Lorenz curve
The Lorenz curve is a graphical representation of income distribution commonly used in the field of economics. While this tool has proven to be helpful in analyzing income inequality, it is important to consider its assumptions and limitations. Understanding these factors is crucial to correctly interpreting the information provided by a Lorenz curve. One of the assumptions underlying the Lorenz curve is that income is the only determinant of economic well-being. This assumption overlooks other factors such as access to education, healthcare, and social welfare systems that also play a significant role in determining an individual’s quality of life. Thus, the Lorenz curve may not fully capture the overall inequality in a society. Another limitation of the Lorenz curve is that it assumes a linear relationship between income and individuals. In reality, income distribution may exhibit non-linear patterns due to various factors such as poverty traps or wealth concentration. These complexities are not adequately represented by the Lorenz curve, potentially leading to an incomplete understanding of income inequality. Furthermore, the Lorenz curve assumes perfect data accuracy and reliability. However, collecting accurate income data can be challenging, especially in countries with informal economies or limited administrative capacities. Inaccurate data may result in misleading Lorenz curves and inaccurate conclusions about income inequality. The Lorenz curve also assumes that individuals can be completely ranked according to their income levels. However, this assumption fails to consider the complexity of individual circumstances and variations in income sources. For example, two individuals with the same reported income may have contrasting financial situations due to other factors such as debt or living expenses. Additionally, the Lorenz curve only focuses on relative income distribution and does not provide a measure of absolute income levels. Consequently, it does not offer insights into the actual standard of living or poverty levels within a society. Therefore, policymakers should use additional measures alongside the Lorenz curve to gain a comprehensive understanding of income inequality. Lastly, the Lorenz curve assumes a static distribution of income, disregarding the dynamics of economic mobility over time. In reality, individuals can move between income groups, and examining only the static distribution may mask the potential for upward or downward mobility within a society. In conclusion, the Lorenz curve is a useful tool for analyzing income inequality, but it is important to keep in mind its assumptions and limitations. By understanding these factors, researchers and policymakers can use the Lorenz curve in conjunction with other indicators to gain a more comprehensive understanding of income distribution and effectively address issues of inequality.
Criticism and controversies surrounding Lorenz curve
Criticism and controversies surrounding Lorenz curve: One of the main criticisms surrounding the use of the Lorenz curve as a tool for measuring income inequality is its heavy reliance on the Gini coefficient. The Gini coefficient, derived from the Lorenz curve, is a numerical representation of income inequality ranging from 0 to 1, with 0 indicating perfect equality and 1 indicating absolute inequality. Some researchers argue that the Gini coefficient oversimplifies the complex nature of income distribution and fails to capture other dimensions of inequality such as wealth, education, and access to basic services. Critics also point out that the Lorenz curve does not take into account factors such as economic growth, changes in productivity, or government policies that can significantly impact income distribution over time. As a static measure, it fails to capture the dynamic nature of income inequality and the complex interplay of various socioeconomic factors. Furthermore, the Lorenz curve assumes that income inequality can be adequately represented by a cumulative distribution curve. However, this assumption can overlook the specific distribution patterns within different income groups. For instance, it may fail to capture the presence of a significant number of individuals or households with extremely high or low incomes, which can skew the overall representation of income distribution. Another criticism of the Lorenz curve is that it tends to ignore the underlying causes and drivers of income inequality. While it provides a snapshot of the distribution of income at a given point in time, it does not offer insights into the factors that contribute to disparities, such as discrimination, lack of access to education or employment opportunities, or systemic economic and social structures. By focusing solely on the shape of the curve, the Lorenz curve fails to provide a comprehensive understanding of the underlying forces that shape income inequality. There are also controversies surrounding the choice of data used to construct the Lorenz curve. For accurate and reliable measurements, a robust and representative dataset is essential. However, data collection methodologies can vary across countries and sources, leading to potential discrepancies and inaccuracies in the measurement of income distribution. This can impact the validity and comparability of Lorenz curves derived from different datasets. In conclusion, while the Lorenz curve is a widely used tool for measuring income inequality, it is not without its limitations and controversies. Critics argue that its reliance on the Gini coefficient, its static nature, and its failure to capture underlying causes of inequality all limit its usefulness. Issues related to data collection and representation further contribute to the ongoing discussion and debate surrounding the Lorenz curve and its effectiveness in capturing the complexity of income inequality.
Definition of Lorenz curve
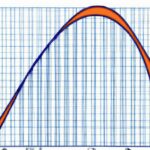
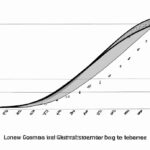
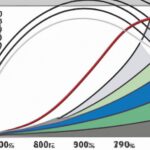
The Lorenz curve is a graphical representation used to depict income or wealth inequality within a given population. It was developed by American economist Max O. Lorenz in 1905 and has since become an essential tool in the field of economics for analyzing income distribution patterns. The Lorenz curve is constructed by plotting the cumulative percentage of total income or wealth held by each segment of the population against the cumulative percentage of the population. In other words, it shows what portion of the total income or wealth is held by different sections of the population, starting from the poorest to the richest. The horizontal axis of the Lorenz curve represents the cumulative percentage of the population, ranging from 0% (representing the poorest individuals) to 100% (representing the richest individuals). The vertical axis represents the cumulative percentage of total income or wealth held by the population, also ranging from 0% to 100%. A perfectly equal distribution of income or wealth would result in a diagonal line on the Lorenz curve, known as the “line of equality.” In such a case, each segment of the population would hold an equal proportion of the total income or wealth. However, in reality, income or wealth distribution tends to be uneven. Consequently, the Lorenz curve generally falls below the line of equality. The further the curve is from the diagonal line, the greater the level of income or wealth inequality within the population. The shape of the Lorenz curve helps economists and policymakers understand the concentration of income or wealth in society. If the curve is closer to the line of equality, it indicates a more equal distribution. Conversely, if the curve is farther away from the line of equality, it suggests a more unequal distribution. Additionally, the Lorenz curve can be used to calculate a summary statistic called the Gini coefficient. The Gini coefficient is a numerical measure of income or wealth inequality derived from the Lorenz curve. It ranges from 0 to 1, where 0 represents perfect equality, and 1 represents maximum inequality. The Lorenz curve, along with the Gini coefficient, provides valuable insights into the distribution of income or wealth in a society. These tools are instrumental in understanding the disparities within populations and formulating policies to address income inequality and promote economic justice.
Purpose and significance of Lorenz curve analysis
The purpose and significance of Lorenz curve analysis lie in its ability to measure income inequality within a population. The Lorenz curve is a graphical representation of the distribution of income or wealth among the members of society. By analyzing the Lorenz curve, researchers and policymakers can gain valuable insights into the level of inequality and devise strategies to address it. One of the primary purposes of the Lorenz curve analysis is to provide a visual representation of income or wealth distribution. The curve allows policymakers to see at a glance how income is distributed across different sections of the population. This information is essential for understanding the extent of inequality present in a given society. Another purpose of the Lorenz curve analysis is to calculate a key inequality measure, known as the Gini coefficient. The Gini coefficient is a numerical value derived from the Lorenz curve that quantifies the level of income inequality within a population. It ranges from 0 to 1, where 0 represents perfect equality and 1 represents extreme inequality. The Gini coefficient allows policymakers to compare inequality over time or across different countries and regions. The significance of Lorenz curve analysis lies in its ability to inform policy decisions and interventions aimed at reducing income inequality. By visualizing the distribution of income or wealth, policymakers can identify which segments of the population are disproportionately affected by inequality and target specific areas or groups for intervention. Furthermore, the Lorenz curve analysis provides a tool for evaluating the effectiveness of redistributive policies and social welfare programs. By comparing the distribution of income before and after implementing such policies, policymakers can assess if the interventions have successfully reduced inequality and improved the well-being of disadvantaged groups. The significance of the Lorenz curve analysis extends beyond economic considerations. High levels of income inequality have been associated with a range of social and health issues, including decreased social mobility, increased crime rates, and poorer overall health outcomes. By using the Lorenz curve analysis to identify and address income inequality, policymakers can work towards creating a more equitable and cohesive society. In summary, the purpose and significance of Lorenz curve analysis are rooted in the need to measure income inequality and inform policy decisions. By providing a visual representation of income or wealth distribution and calculating the Gini coefficient, the Lorenz curve analysis enables policymakers to identify and address inequality. Recognizing the significance of income inequality in various social and economic issues, the use of the Lorenz curve analysis can contribute to the development of more equitable societies.