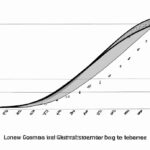
Measuring income inequality reveals the stark reality of wealth distribution. The Lorenz curve is a useful tool in this analysis, visually representing the income gap. It plots the cumulative share of income against the cumulative share of the population. A perfectly equal society would have a straight line, while a skewed distribution results in a curved line. The further the curve is from the straight line, the more unevenly income is distributed. This measurement fosters understanding, sparks discussions, and encourages policymakers to address inequality. By studying the Lorenz curve, we can strive for a fairer society, where wealth and opportunities are more equitably shared among the population.
Table of Contents
- Data collection methods for measuring income inequality
- Definition of income inequality
- Explanation of the Lorenz curve
- Interpretation of the Lorenz curve
- Limitations and criticisms of using the Lorenz curve to measure income inequality
(Lorenz Curve and Gini Coefficient – Measures of Income Inequality)
Measuring income inequality is important to understand the distribution of wealth in a society. One commonly used tool for this purpose is the Lorenz curve. The Lorenz curve is a graphical representation that compares the cumulative share of income to the cumulative share of the population.
To construct a Lorenz curve, we first arrange the population from poorest to richest. Then, we calculate the cumulative share of income for each group and plot it against the cumulative share of the population.
The Lorenz curve provides a visual depiction of income inequality. If the curve lies closer to the diagonal line, it indicates a more equal distribution of income. In contrast, if the curve bends away from the diagonal line, it signifies higher income inequality.
The Gini coefficient is another measure derived from the Lorenz curve. It quantifies income inequality numerically, with values ranging from 0 to 1. A Gini coefficient of 0 represents perfect income equality, while a coefficient of 1 indicates extreme inequality.
By using the Lorenz curve and Gini coefficient, policymakers can assess the effectiveness of economic policies aimed at reducing income disparities. These measures help identify areas where wealth distribution is inequitable and implement targeted interventions.
In conclusion, the Lorenz curve is a valuable tool for measuring income inequality. Its graphical representation offers insights into the distribution of wealth, enabling policymakers to formulate appropriate strategies for a more equitable society.
Data collection methods for measuring income inequality
Data collection methods for measuring income inequality play a crucial role in quantifying and understanding the disparities that exist within a society. These methods provide valuable insights into the distribution of wealth and help policymakers formulate effective strategies to address the issue.
One commonly used method is survey-based data collection, where households are asked to provide information about their income. Through carefully designed questionnaires and interviews, researchers can obtain valuable data on individual or household income, which can then be used to calculate various inequality measures.
Another approach is administrative data collection, which involves utilizing existing records such as tax returns or social security data. These records provide a comprehensive and reliable source of income information, as they are typically collected for administrative purposes. Administrative data collection is often less costly and time-consuming than surveys, making it an attractive option for researchers.
Additionally, researchers can employ direct observation techniques to gather income data. This method involves observing specific economic transactions or activities that reveal income levels, such as wage records or business receipts. Direct observation can offer a more accurate picture of income distribution, especially in cases where individuals may underreport their incomes.
Furthermore, data collection methods can also involve using proxy variables to estimate income inequality indirectly. For example, researchers may use indicators such as education levels, housing conditions, or access to healthcare as proxies for income. While these proxies may not provide a precise measure of income inequality, they can give insights into the disparities that exist within different socioeconomic groups.
It is important to note that each data collection method has its advantages and limitations. Surveys, for instance, rely on individuals providing accurate and honest information, which can be influenced by social desirability bias. Administrative data may not capture the full range of income sources for some individuals, leading to an underestimation of inequality. Direct observation methods, while accurate, can be time-consuming and expensive to implement on a large scale.
In conclusion, data collection methods for measuring income inequality are essential tools for understanding and addressing wealth disparities within a society. Whether through surveys, administrative records, direct observation, or proxy variables, these methods provide valuable insights into the distribution of income and are vital in informing policymakers and researchers in their pursuit of a more equitable society.
Definition of income inequality
Income inequality refers to the unequal distribution of income among individuals in a society. It is a measure of the disparities in earnings between different segments of the population. While some individuals may have high incomes, others may struggle to make ends meet, resulting in a significant gap between the rich and the poor.
The Lorenz curve is a graphical representation used to measure income inequality. It compares the cumulative percentage of income received with the cumulative percentage of the population. The curve starts at the origin, representing perfect equality, where every individual earns an equal share of the total income. As the curve moves away from the origin, it signifies increasing inequality.
The shape of the Lorenz curve provides insight into the distribution of income. A curved line closer to the 45-degree line indicates a more equal distribution, while a curve that bends away from the line suggests greater inequality. The further the Lorenz curve deviates from the line, the higher the level of income inequality.
Income inequality has far-reaching implications for society. It can lead to social unrest, political instability, and economic inefficiency. Inequality hampers social mobility, making it difficult for individuals from disadvantaged backgrounds to improve their economic situation. It also impacts access to basic necessities such as healthcare, education, and housing, perpetuating the cycle of poverty.
Various factors contribute to income inequality. One significant factor is differences in education and skills. Individuals with higher levels of education and specialized skills are generally able to secure higher-paying jobs. Additionally, globalization and technological advancements have disproportionately benefited certain industries and individuals, further exacerbating income disparities.
Addressing income inequality requires a multi-faceted approach. Policies that promote inclusive economic growth, access to quality education, and skill development can help reduce income disparities. Progressive tax systems and social safety nets can also play a role in redistributing wealth and providing a safety net for the most vulnerable members of society.
In conclusion, income inequality refers to the uneven distribution of income within a society. The Lorenz curve is a useful tool for measuring and visualizing income inequality. It is essential to address this issue to ensure a fair and equitable society where everyone has equal opportunities to succeed. By implementing policies that foster inclusive growth and provide social support, we can work towards reducing income inequality and creating a more just society.
Explanation of the Lorenz curve
Income inequality is a significant socio-economic issue that affects nations worldwide. To understand and measure income inequality, researchers and economists often use the Lorenz curve. The Lorenz curve is a graphical representation that provides insights into the distribution of income within a population.
The curve itself is a line that plots the cumulative percentage of a population’s income on the horizontal axis against the cumulative percentage of the population on the vertical axis. This type of curve allows for a visual representation of how income is distributed among different sections of a population.
In an ideal scenario, where income is distributed equally, the Lorenz curve would be a straight 45-degree line. However, in reality, income distribution is often uneven, resulting in a curve that deviates from the ideal line.
The Lorenz curve allows researchers to identify and measure income inequality by examining the extent to which the curve deviates from the ideal line. The further the curve is from the ideal line, the higher the income inequality within the population.
A key metric derived from the Lorenz curve is the Gini coefficient. The Gini coefficient, a numerical representation of income inequality, is calculated as the ratio of the area between the Lorenz curve and the 45-degree line to the total area under the 45-degree line. The coefficient ranges between 0 and 1, with higher values indicating higher income inequality.
By using the Lorenz curve and the Gini coefficient, policymakers can assess the level of income inequality within a society. This information can guide the development and implementation of policies aimed at reducing income disparities and promoting a more equitable distribution of resources.
Moreover, the Lorenz curve provides a useful tool for comparing income inequality across different countries or regions. By analyzing multiple curves, researchers can gain insights into the disparities between different population groups and evaluate the effectiveness of policies implemented to address income inequality.
In conclusion, the Lorenz curve is a valuable tool for measuring income inequality, providing a visual representation of income distribution within a population. Through the Gini coefficient, policymakers can assess the level of income disparities and formulate targeted policies to promote greater economic equity. By utilizing the insights gained from the Lorenz curve, efforts can be made to create more inclusive societies where wealth and opportunities are more evenly distributed.
Interpretation of the Lorenz curve
The Lorenz curve is a graphical representation of income inequality within a population. It provides a visual tool to assess the distribution of wealth and the disparity between different segments of society. By plotting the cumulative percentage of income against the cumulative percentage of the population, the curve illustrates the extent to which income is concentrated or spread out.
When interpreting the Lorenz curve, the diagonal line represents perfect equality, where each person in the population receives an equal share of the total income. Any deviation from this line indicates inequality. The further the Lorenz curve bows away from the diagonal, the greater the income inequality.
To quantify the level of inequality, an index called the Gini coefficient is often used. It measures the area between the Lorenz curve and the diagonal line, with values ranging from 0 to 1. A Gini coefficient of 0 indicates perfect equality, while a coefficient of 1 represents extreme inequality, where one person holds all the income.
Analyzing the shape of the Lorenz curve can provide insight into the nature of inequality. For instance, a concave curve suggests a relatively equal distribution of wealth, with the majority of the population receiving similar income levels. On the other hand, a convex curve indicates a more unequal distribution, with a small percentage of individuals holding a disproportionately large share of the total income.
The Lorenz curve also enables comparisons across countries and over time. By examining different curves, policymakers and researchers can assess the effectiveness of policies aimed at reducing inequality. For example, a country that experiences an outward shift of its Lorenz curve over time indicates worsening income inequality.
Furthermore, the Lorenz curve helps identify specific areas where income inequality is most prevalent. If the curve bows significantly in the lower segments, it suggests that wealth is concentrated among a few affluent individuals. Conversely, if the curve bows in the higher segments, it indicates a wider distribution of income and less inequality.
In conclusion, the Lorenz curve provides a valuable tool for measuring and interpreting income inequality. Its visualization allows for easy comprehension of the distribution of wealth within a population. By analyzing the curve’s shape and calculating the Gini coefficient, policymakers and researchers can gain insights into the extent and nature of inequality, facilitating targeted interventions to address this pressing issue.
Limitations and criticisms of using the Lorenz curve to measure income inequality
The Lorenz curve is a widely used tool for measuring income inequality. However, it is important to recognize its limitations and criticisms.
One limitation is that the Lorenz curve only provides a snapshot of income inequality at a particular point in time. It does not capture changes in inequality over time, which is important for understanding trends and patterns. Additionally, the Lorenz curve assumes that everyone in the population being measured is part of the income distribution, which may not be the case if certain groups are excluded or underrepresented.
Another criticism of the Lorenz curve is that it relies on self-reported income data, which can be unreliable and subject to biases. People may underreport their income or fail to report certain sources of income, leading to an inaccurate representation of inequality. In addition, the Lorenz curve does not take into account non-monetary forms of inequality, such as disparities in access to healthcare or education.
Furthermore, the Lorenz curve assumes that all income is equally distributed within each income group, which may not be realistic. In reality, there may be a wide variation in income within each group, leading to a more unequal distribution than the curve suggests.
The construction of the Lorenz curve also requires the assumption of perfect information, meaning that individuals are aware of the income distribution and make choices accordingly. However, in practice, people may not have accurate information about the income of others, which can affect their decisions and behaviors.
Additionally, the Lorenz curve does not consider factors such as wealth accumulation, which can contribute to overall inequality. Wealth disparities can have a significant impact on socio-economic mobility and opportunities.
In conclusion, while the Lorenz curve is a useful tool for measuring income inequality, it is important to recognize its limitations and criticisms. It provides a snapshot of inequality at a specific point in time but does not capture trends or changes over time. The reliance on self-reported income data and the assumption of perfect information are also potential weaknesses. Non-monetary forms of inequality and factors such as wealth accumulation are not taken into account. Therefore, it is essential to consider these limitations when using the Lorenz curve as a measure of income inequality and to supplement it with other indicators for a more comprehensive understanding.