The Gini coefficient measures income inequality within a population. It is calculated using a formula that compares the cumulative income shares to the cumulative population shares. To calculate it, first arrange the population in ascending order by income. Then, calculate the cumulative population percentage and cumulative income percentage at each income level. Next, subtract the cumulative population percentage from the cumulative income percentage to get the Gini coefficient values at each income level. Finally, sum up the Gini coefficient values and divide by the total number of income levels. A Gini coefficient close to 0 represents perfect equality, while a coefficient close to 1 indicates extreme inequality. The calculation method provides valuable insights into the income distribution within a society.
Table of Contents
- Applications and relevance of Gini coefficient.
- Calculation steps and methodology
- Definition and Formula of Gini coefficient
- Interpretation and limitations of Gini coefficient
- Introduction
(How to Calculate the Gini Coefficient)
The calculation methodology of the Gini coefficient measures inequality within a population. It provides a numerical value ranging from 0 to 1, where 0 represents perfect equality, and 1 represents extreme inequality.
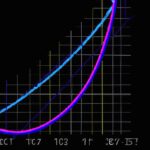
To calculate the Gini coefficient, one needs data on the distribution of income or any other variable of interest. The first step involves arranging the data in ascending order. Then, a Lorenz curve is constructed by plotting the cumulative percentage of the variable against the cumulative percentage of the population. The Lorenz curve starts at the origin and ends at the point where 100% of the population holds 100% of the variable.
The Gini coefficient is calculated as the area between the Lorenz curve and the line of perfect equality, divided by the total area under the line of perfect equality. This value is then subtracted from 1 to obtain the Gini coefficient.
A Gini coefficient of 0 indicates perfect equality, where every individual has the same share of the variable being measured. On the other hand, a Gini coefficient of 1 represents extreme inequality, with one individual accumulating all the variable’s value.
The Gini coefficient is widely used to analyze income distribution, but it can also be applied to assess inequality in other areas such as education or wealth distribution.
By using this simple yet powerful calculation methodology, policymakers and researchers can gain valuable insights into the level of inequality and make informed decisions to promote a more equitable society.
Applications and relevance of Gini coefficient.
The Gini coefficient is widely used to measure and analyze income inequality within a population. It provides valuable insights into the distribution of wealth and income among individuals or groups, making it a crucial tool for policymakers and researchers alike.
One of the main applications of the Gini coefficient is in studying economic development. By comparing Gini coefficients across different countries, economists can assess the level of inequality in each nation and identify potential areas for improvement. This information is particularly useful in formulating policies aimed at reducing poverty and promoting social welfare.
Another important application of the Gini coefficient is in assessing the impact of taxation and social welfare programs. By calculating the Gini coefficient before and after the implementation of these policies, policymakers can evaluate their effectiveness in redistributing wealth and reducing inequality. This allows for a more targeted approach to poverty alleviation, ensuring that resources are allocated where they are most needed.
The Gini coefficient is also relevant in the field of healthcare research. By analyzing the relationship between income inequality and health outcomes, researchers can identify potential disparities in access to healthcare services. This can inform the development of public health interventions, ensuring that vulnerable populations receive the necessary medical care and reducing health inequalities.
Furthermore, the Gini coefficient is increasingly being used in environmental studies. By incorporating environmental indicators into the calculation of the Gini coefficient, researchers can assess the environmental inequality within a population. This provides insights into the disproportionate burden of pollution and resource depletion on marginalized communities, highlighting the need for sustainable and equitable environmental policies.
In addition to its applications in research and policymaking, the Gini coefficient is also essential in public discourse. It serves as a valuable tool for raising awareness about income inequality and promoting social justice. By visualizing the distribution of wealth and income in a society, the Gini coefficient can generate public support for policies aimed at reducing inequality and fostering inclusive growth.
Overall, the Gini coefficient plays a crucial role in understanding and addressing income inequality. Its applications span various fields, from economic development and taxation to healthcare and environmental studies. By providing a comprehensive measure of inequality, the Gini coefficient empowers policymakers and researchers to make informed decisions that promote a more equitable and just society.
Calculation steps and methodology
Calculation steps and methodology for Gini coefficient are important in measuring income inequality. The Gini coefficient, a statistical tool, provides valuable insights into the distribution of wealth within a society. With a value ranging from 0 to 1, a higher Gini coefficient signifies greater inequality.
To calculate the Gini coefficient, follow these steps:
1. First, organize data on income or wealth distribution by arranging individuals or households from lowest to highest. This step ensures a clear understanding of the distribution pattern.
2. Next, create a Lorenz curve, graphically representing the cumulative percentage of the population against the cumulative percentage of income or wealth. The aim is to determine the proportion of income held by different segments of the population.
3. Calculate the area between the Lorenz curve and the line of perfect equality (a straight line diagonal from the bottom-left corner to the top-right corner of the graph). This area represents income inequality.
4. Divide the area obtained in step 3 by the total area under the line of perfect equality. This division yields the Gini coefficient.
The methodology for calculating the Gini coefficient ensures accurate results by providing a standardized approach. It allows for consistent comparison between different societies, regions, or time periods.
By using commonly available data, such as income data from census surveys or national economic accounts, policymakers and researchers can calculate the Gini coefficient to assess the degree of income inequality, identifying areas of concern and potential policy interventions.
The Gini coefficient calculation methodology is an essential tool in highlighting inequality and its implications. It enables policymakers to make informed decisions by quantifying the distribution of income or wealth within a society.
Understanding the calculation steps and methodology requires basic statistical knowledge. However, it is a crucial concept that contributes to a comprehensive understanding of income inequality and societal well-being.
In conclusion, the calculation steps and methodology of the Gini coefficient provide valuable insights into income inequality. By following a standardized approach and organizing data effectively, policymakers and researchers can accurately quantify income distribution patterns. This information is vital for addressing societal disparities and designing effective policies to promote equity and inclusion.
Definition and Formula of Gini coefficient
The Gini coefficient is a measure that quantifies the degree of income inequality within a population. It is widely used by economists, policymakers, and social scientists to assess the distribution of wealth in a country.
The formula for calculating the Gini coefficient is relatively simple. It involves comparing the Lorenz curve, which plots the cumulative share of total income against the cumulative percentage of the population, to the hypothetical line of perfect equality. The Gini coefficient is calculated as the area between these two lines divided by the total area under the perfect equality line.
By using this formula, the Gini coefficient provides a numerical value between 0 and 1. A coefficient of 0 indicates perfect equality, meaning that every person in the population has an equal share of the total income. On the other hand, a coefficient of 1 represents extreme inequality, where one person has all the income and everyone else has none.
Understanding the Gini coefficient helps policymakers make informed decisions regarding income distribution and poverty alleviation programs. It allows them to identify areas where income inequality is particularly prevalent and develop strategies to address these disparities.
For example, if a country has a high Gini coefficient, policymakers may consider implementing policies such as progressive taxation, increased investment in education and healthcare, and the creation of job opportunities in low-income areas. These measures aim to redistribute wealth and provide equal opportunities for all individuals, thereby reducing income inequality.
However, it is important to note that the Gini coefficient has its limitations. It does not capture factors such as access to education, healthcare, and social mobility, which also play a significant role in determining a person’s economic well-being. Additionally, it is a snapshot measure and does not consider changes in income distribution over time.
In conclusion, the Gini coefficient is a valuable tool for measuring income inequality within a population. Its formula provides a straightforward way to calculate and compare levels of inequality between different countries and regions. By understanding and utilizing the Gini coefficient, policymakers can work towards creating a more equitable society for all.
Interpretation and limitations of Gini coefficient
Interpretation and limitations of Gini coefficient can provide a deeper understanding of income distribution. The Gini coefficient is a statistical measure commonly used to quantify inequality within a given population or group. It ranges from 0 to 1, where 0 represents perfect equality and 1 represents extreme inequality. However, it is important to interpret the Gini coefficient cautiously, as it has some limitations.
Firstly, the Gini coefficient does not reveal the actual income levels or the reasons behind the inequality. While it shows the extent of inequality, it does not provide any information about the income distribution curve or the income of each individual. Therefore, it is crucial to consider additional data and indicators when analyzing income inequality.
Secondly, the Gini coefficient assumes that all income is derived from a single source. In reality, individuals often have multiple sources of income, such as wages, investments, and government benefits. This assumption can oversimplify the complexity of income distribution and may not accurately reflect the true level of inequality.
Furthermore, the Gini coefficient does not consider non-monetary aspects of inequality, such as access to education, healthcare, or social mobility. These non-monetary factors can significantly impact individuals’ well-being and opportunities, but they are not captured by the Gini coefficient alone. Therefore, it is important to complement the Gini coefficient with other indicators to gain a comprehensive understanding of inequality.
Additionally, the Gini coefficient may not be suitable for comparing inequality across different countries or populations. It is sensitive to the size of the population and can be influenced by outliers or extreme values. Therefore, caution must be exercised when comparing Gini coefficients across different contexts, as variations in data collection methods, population sizes, and economic structures can affect the results.
In conclusion, while the Gini coefficient is a useful metric for measuring income inequality, its interpretation should take into account its limitations. It does not provide a complete picture of income distribution, fails to consider non-monetary aspects of inequality, and may not be suitable for cross-country comparisons. To gain a comprehensive understanding of inequality, it is essential to complement the Gini coefficient with other indicators and contextual information.
Introduction
The Gini coefficient is a statistical measure that quantifies the level of economic inequality within a society. It is widely used to assess income distribution and to compare it across different countries and regions. The calculation methodology of the Gini coefficient involves a mathematical formula that takes into account the distribution of income among the population.
To calculate the Gini coefficient, one first needs to sort the income data from lowest to highest. Then, a cumulative distribution function is constructed by allocating the percentage of total income to each corresponding percentile of the population. This cumulative distribution curve represents the income distribution within the society.
The Gini coefficient is derived from the Lorenz curve, which is a graphical representation of the income distribution. The Lorenz curve plots the cumulative percentage of total income received by the corresponding cumulative percentage of the population. The Gini coefficient is calculated as the area between the Lorenz curve and the line of perfect equality, which is a 45-degree line representing equal income distribution.
The Gini coefficient ranges from 0 to 1, where 0 represents perfect equality (all individuals have the same income) and 1 represents maximum inequality (one individual has all the income). A Gini coefficient of 0.5 is often considered as a threshold for high income inequality.
The calculation of the Gini coefficient provides policymakers, researchers, and organizations with a valuable tool to assess the level of inequality within a society and to monitor changes over time. It helps identify areas where wealth is concentrated and where redistribution measures may be necessary. Moreover, the Gini coefficient allows for international comparisons, enabling policymakers to benchmark their country’s income distribution against global standards.
While the Gini coefficient provides a useful summary measure of income inequality, it has its limitations. It is sensitive to changes in the middle-income groups, while disregarding extreme values at the top and bottom percentiles. Additionally, it only captures income disparities and does not account for other dimensions of inequality such as wealth or access to basic services.
In conclusion, the calculation methodology of the Gini coefficient offers a systematic approach to measure and analyze income inequality. It provides insights into the distribution of income within a society, facilitating policy interventions aimed at reducing inequality and promoting inclusive growth. However, it is essential to consider the limitations of the Gini coefficient and complement it with other indicators to gain a comprehensive understanding of the multifaceted nature of inequality.